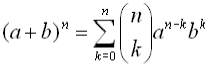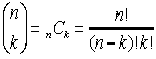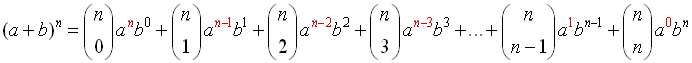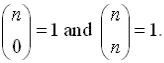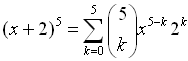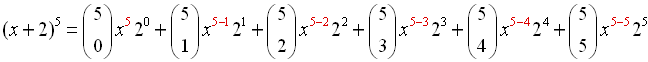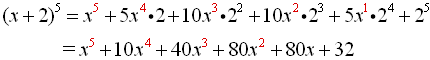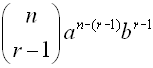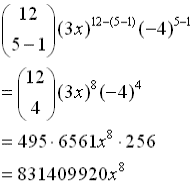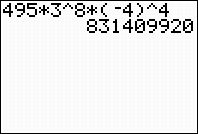|
Binomial Theorem
(or Binomial Expansion Theorem)
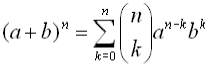 |
|
Most of the syntax used in this theorem should
look familiar. The
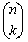 notation is
just another way of writing a combination such as n
C k (read "n choose k"). notation is
just another way of writing a combination such as n
C k (read "n choose k").
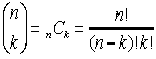 |
Example 1: Expand 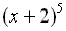 . . |
|
Let a = x, b = 2, n = 5 and
substitute.
(Do not substitute a value for k.) |
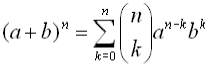
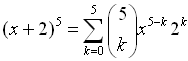
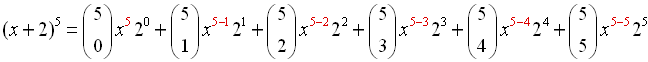
Now, grab your graphing calculator to find those
combination values.
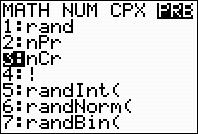
Method 1: Use
the graphing calculator to evaluate the
combinations on the home screen. Remember: Enter the top value of the
combination FIRST. Then hit MATH key, arrow right (or left) to PRB heading, and choose #3 nCr.
Now, enter the bottom value of the combination.
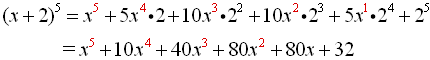
Method 2: Use
the graphing calculator to evaluate the
combinations under the lists.
|
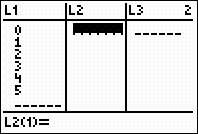
In L1, enter the values 0 through
the power to which the binomial
is raised, in this case 5.
|
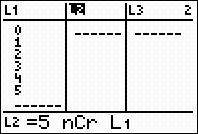
In L2, enter the combination
formula, using the power of the
binomial as the starting value,
and the entries from L1 as the
ending values.
|
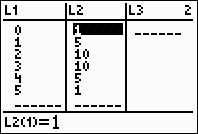
The coefficients from the
combinations will appear
in L2.
|
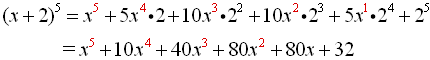
Finding a
Particular Term in a Binomial Expansion
|
The
r th term of the expansion of 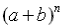 is: is:
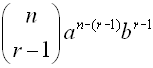 |