Linear-Quadratic Systems
(Line - Parabola, Line - Circle)
|
The graphing capabilities of the calculator will be put to use to solve linear-quadratic systems.
This solution method will simply graph the equations and find the points of intersections,
if such points exist.
Line and Parabola:
A quadratic equation is defined as
an equation of degree two.
In a linear- quadratic system where only one variable in the quadratic is squared,
the graphs will be a parabola and a straight line.
Linear - quadratic system - Line and Parabola:
(where only one variable is squared) |
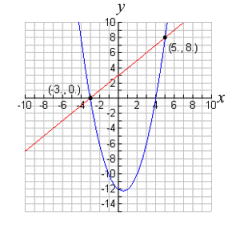
When graphing a parabola and a straight line on the same set of axes, three situations are possible.
 |
 |
 |
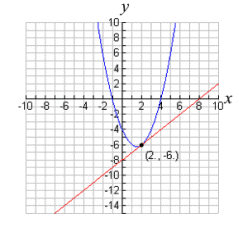
| The equations
will intersect in two locations. Two real solutions. |
The equations
will intersect in one location. One real solution. |
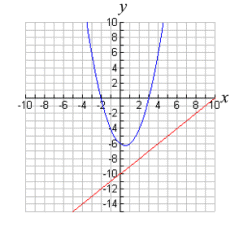
The equations will not
intersect.
No real solutions. |
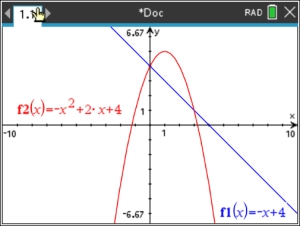
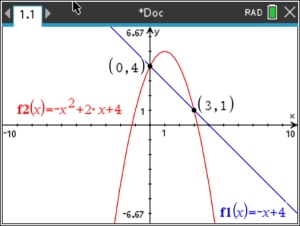
| Solve graphically: |
y = -x2 + 2x + 4 (quadratic -
parabola)
x + y = 4 (linear) |
| 1. |
• If needed rewrite the equation so they are in "y =" form.
• In this example, change the linear equation
to "y=" form. |
y = -x + 4 |
| 2. |
Enter
the equations as "f 1(x)" and
"f 2(x)".
Be sure you can see the intersection points on the screen. Adjust the window if needed.
|
|
| 3. |
Use the Intersection option.
 , #6 Analyze Graph,
#4 Intersection
Repeat for each intersection point.
Solution: (0,4) and (3,1) |
 |
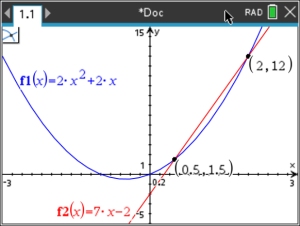
Solve graphically:
(with GEOMETRY option) |
y = 2x2 + 2x (quadratic -
parabola)
y = 7x - 2 (linear) |
This is another alternative to locating intersections points.
* |
Using
a GEOMETRY Option for Intersection |
| |
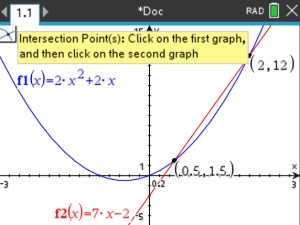
Let's look at another example.
This time we will use a Geometry option.
Start a new Document:  Graph
1. Prepare the graph,
Set f 1(x) = 2x2 + 2x and f 2(x) = 7x - 2
2. #8 Geometry, #1 Points & Lines,
#4 Intersection Points
3.
Click on BOTH graphs.
4. Both intersection points will appear with their coordinates.
ANSWER: (0.5,1.5) and (2,12).
Note: If you forget what to do after step 3, click on the icon in the upper left corner of the screen, and a hint will drop down (in yellow). |
Window [-3,3] x [-5,15]
|
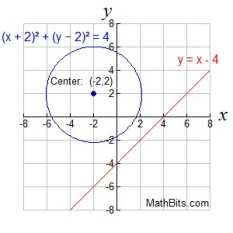
Line and Circle:
In a linear- quadratic system where BOTH variables in the quadratic are squared,
the graphs will be a circle and a straight line.
Linear - quadratic system - Line and Circle:
(where both
variables are squared) |
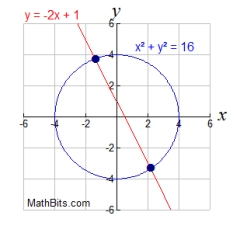
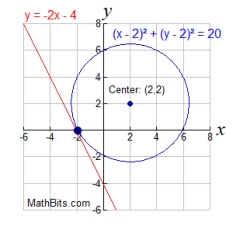
Like with the parabola, the graphs below show that when a line and a circle
are graphed on the same set of axes, three situations are possible.
 |
 |
 |
| The equations will intersect in two locations.
Two real solutions. |
The equations will intersect in one location (a tangent). One real solution. |
The equations will not intersect.
No real solutions. |
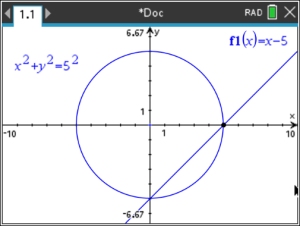
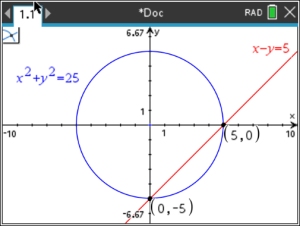
| Solve graphically: |
x2 +
y2 = 25 (quadratic - circle)
x - y = 5 (linear) |
|
This solution will use the line as a "function", and the circle as a "relation".
| 1. |
• When graphing a line and a circle on the same grid, it will be easier if the line is graphed first.
•
Rewrite the linear equation into "y =" form.
•
Enter
the equation as "f 1(x)". |
Graph the "line" first!
y = x - 5 |
| 2. |
We know that this circle has a center at the origin, (0,0), and a radius of 5.
(h,k) = (0,0) and r = 5
, #3 Graph Entry/Edit, #3 Equations Template, #3 Circle, #1 Center form
Adjust window if needed to see intersection points. |
|
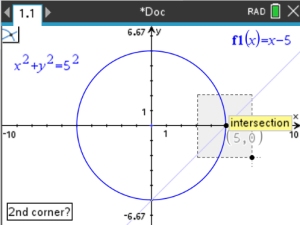
| 3. |
Use the Intersection option.
, #6 Analyze Graph,
#4 Intersection
In this situation, the "intersection" option will create a "box" around the point.
Click to lock a corner of the box.
Drag to form the box.
Repeat for each intersection point. |
 |
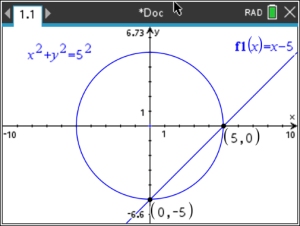
| 4. |
Solution: (0,-5) and (5,0) |
 |
Let's take another look at this problem.
This time BOTH the line and the circle will be entered as "relations".
Then the GEOMETRY option will be used to find the intersection points.
* |
Using
a GEOMETRY Option for Intersection |
| |
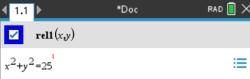
Enter both the line and the circle as "relations":
Move to f 1(x)=, but instead of entering an equation, hit
#3 Graph Entry/Edit, #2 Relation.
The Entry will now appear in "relation" mode.
Enter the two equations.
Now, for the intersection points:
#8 Geometry, #1 Points & Lines,
#4 Intersection Points
Click on BOTH graphs.
Both intersection points will appear with their coordinates.
ANSWER: (0,-5) and (5,0) |
Entry:
|
Table of Contents | MathBits.com | Terms of Use
|
