|
Enable the Use of Complex Numbers
 , #5 Settings, #2 Document Setting , #5 Settings, #2 Document Setting
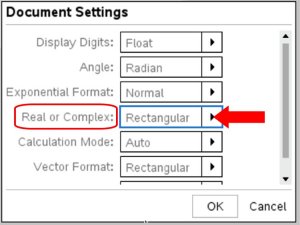
Under Real or Complex; Choose "Rectangular"
Hit OK.
The "rectangular" mode is this calculator's form of "a+bi" mode.
Changing the "Document Setting" will keep your calculator in "Complex mode" for upcoming work.
The new settings become "default" settings.
(There is no "Make Default" button on the TI-Nspire CX II calculator.)
Since "Complex" mode includes "Real" mode,
keeping your calculator in "Complex" mode will be advantageous for work with Algebra 2.
|
Entering Complex Numbers
(How to enter the imaginary i )
NOTE: The letter "i" typed off the alphabetic keys is NOT an activated imaginary "i".
Method 1: Pres the  key key
and this chart will appear. Choose i.
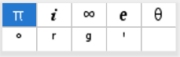
Method 2: use symbols' chart
Press  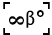
Note: 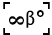 is found above is found above  |
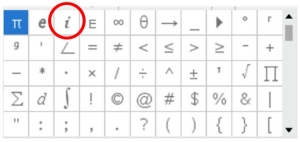
Method 3: if you type "@i" and hit  you will activate imaginary i you will activate imaginary i
The @ comes from the symbol chart and the i is from the keypad. When you hit "enter" the @ symbol will disappear, leaving an activated i.
|

